|
| Consider a circle O with a diameter AB. Draw a second circle with diameter AC, such that C is on AB in circle O. Draw an isosceles triangle with base CB and third vertex on circle O. Draw a third circle (X), tangent to the first three figures. Prove that the line from C to the center of circle X is perpendicular to AB. |
Solutions were received from several people. Each is listed below with their contributed solution. These are ordered only by date received:
Notations:
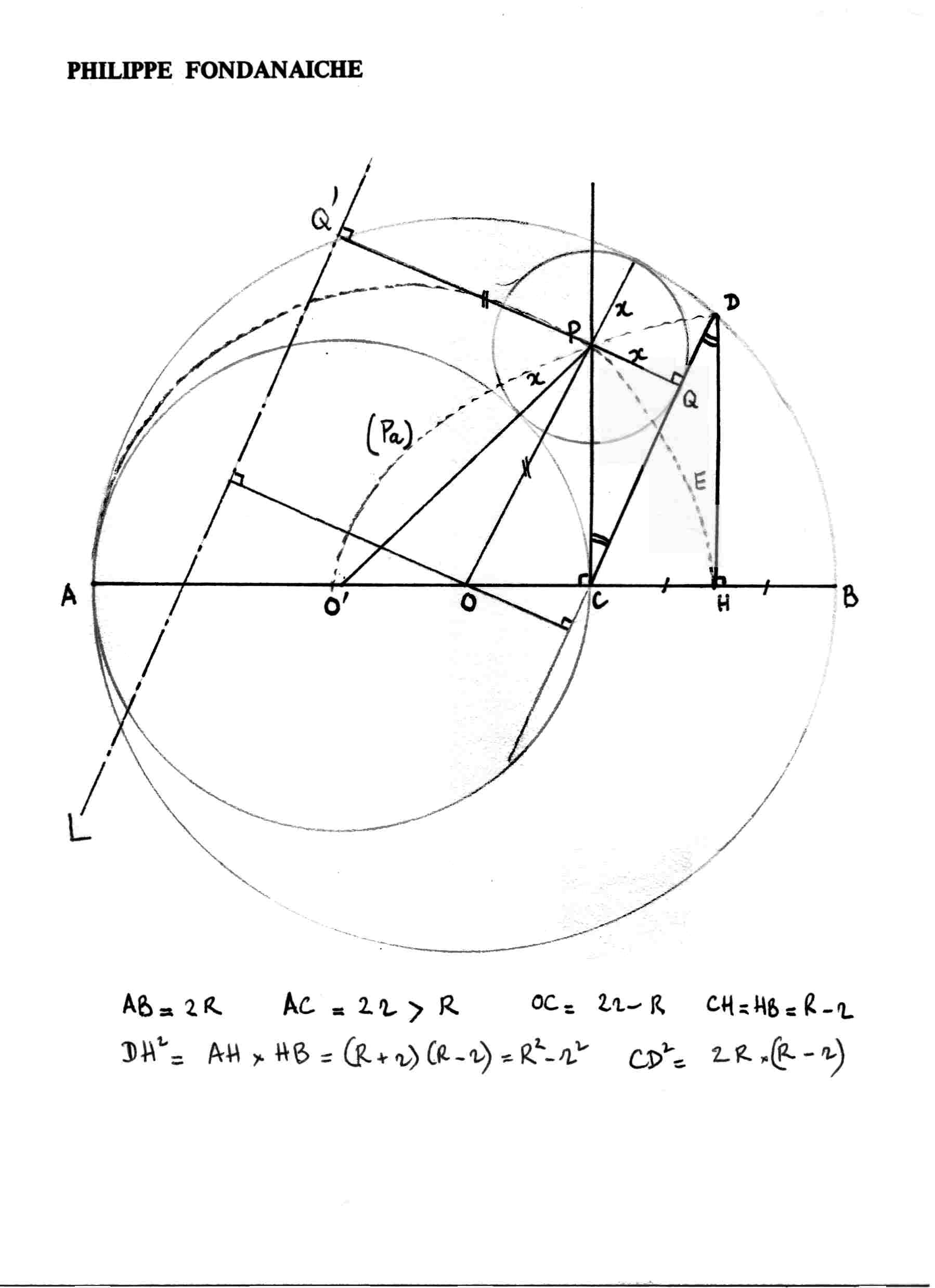
Let the circle (O) of center O and diameter AB=2*R and the circle (O') of
center O' and diameter AC=2*r. See the figure in the attached file.
We assume that 2*r > R. If not the reasoning remains the same.
H is the midpoint of CB and D is the third vertex of the isosceles triangle
DCB with base CB.
Then CB = 2*(R-r)
OC = 2*r - R
CH = HB = R-r
DH^2 = AH*HB = (R+r)*(R-r) = R^2-r^2
CD^2 = CH^2 + DH^2 = 2*R*(R-r)
Let x the radius and P the center of the circle (X) tangent to (O), (O')
and CD. Let the line L // CD such that the distance between the two lines is
R and the circle (X) is between L and CD. Q and Q' are the respective foots
of P on CD and L.
Preliminary remark
P is at the intersection of an ellipse and of a parabola.
1) the locus of the points M which are the centers of the circles tangent
to (O) and (O') is an ellipse (E) with foci O and O'.
Indeed MO+MO' = R+x+r-x = R+r = constant term
2) the locus of the points M which are the centers oft he circles tangent
to (O) and CD is the parabola (Pa) of focus O and directrix L.
Indeed MO+MQ = (R-x) + x = R,then MQ' = MO = R-x.
Therefore P is at the intersection of (E) and (Pa) and P is unique
Demonstration
Let P' at the intersection of (Pa) and of the perpendicular to AB at
the point C. Q' is the projection of P' on CD. Let x' = P'Q' and y' = P'C
P'Q'C and DCH are similar.So x'/y' = CH/CD = sqrt[ (R-r)/2*R ] (a)
On the other hand, with the right-angle triangle OCP',
OP^2 = OC^2 + CP'^2 or (R-x')^2 = (2*r - R)^2 + y'^2 (b)
The two equations (a) and (b) lead to a quadratic equation in x'
whose unique solution is x' = 2*r*(R-r)/(R+r).
Then y' = 2*r*sqrt[2*R*(R-r)]/(R+r)
Moreover with the right-angle triangle O'CP', we have
P'O' = sqrt( y'^2 + r^2) = sqrt( 8*r^2*R*(R-r)/(R+r)^2 + r^2 ) .
So P'O' = (3*R-r)*r/(R+r)
and we can check that P'O' = r + 2*r*(R-r)/(R+r) = r +x'.
As a consequence the circle of center P' which is tangent to (O)
and CD by construction is also tangent to (O'). As P is unique,
P' and P are the same point. and PC (as P'C) is perpendicular to AB.
Referring to:
Dane Brooke: Consider a circle of radius A centered at (-A, 0) [in place of your left side interior circle] and Consider a circle of radius (A+B) centered at (B-A, 0) [in place of your exterior circle] and Locate a circle of radius R centered at (0, D) tangent to both former circles. Evidently 1) A^2 + D^2 = (A + R)^2 whence 2) D^2 = R^2 + 2AR and 3) (B - A)^2 + D^2 = (A + B - R)^2 whence 4) R = (2AB)/(2A + B) A line from the origin, with positive slope, is tangent to the third circle at C and intersects the second circle at (X, H). We have 5) H^2 = (A + B)^2 - (B - A + X)^2 so that 6) H = sqrt(4AB + 2(A - B)X) The triangle with vertices (0, 0), C, (0, D) is similar to the one with vertices (0, 0), (X, H) and (X, 0). In the former the length of the leg from (0, 0) to C is 7) sqrt(2AR) and so 8) H/X = sqrt(2A/R) = sqrt((2A + B)/B) = sqrt((4AB + 2(A - B)X)/X^2) The positive solution for X is indeed X = B, essentially establishing the proof you wanted.
Jimmy Chng Gim Hong A need to know about the construction of the figure appeared in the question One way of constructing the figures of this question, it can be done by drawing an isosceles triangle first (i.e. with base CB). Note that angle CZB (let Z be the vertex) of this isosceles triangle must be smaller than 60 degrees if C is not the center of circle O. CZB is 60 degrees only when C is at the center, and according to the question angles ZCB and ZBC are to the same, thus when CZB is 60 degrees, an equilateral triangle is formed. The radius of circle O, can be calculated by: ZB/sin ZOB=Radius/sin ZBC (assuming O is the center of circle O). Notice that triangles OZB and the original ZCB are similar triangles, thus angle CZB=ZOB. When we know the radius of circle O, we can draw the 2nd circle. To draw the 3rd circle (circle X), we can do it simply by drawing another similar triangle of OZB (ZCB) with its vertex pointing at C first, and thereafter, circle X will be within this 3rd similar triangle. NOTE: As mentioned above, triangles CZB, OZB, and the 3rd triangle with vertex at point C are similar triangles (isosceles triangles). Circle X is within the 3rd triangle; hence, if I make a slight change to my drawings, triangles CZB, OZB and the 3rd one become equilateral triangles; angles ZCB and ZBC are the same. (Triangle OZB=CZB, C is now at the center of circle O) circle X will be still inside another similar/equilateral triangle (but this time, its vertex will be pointing at C) and whether the line joining C to the center of circle X is perpendicular to diameter AB or not, the rule remains unchanged. Proving When triangle CZB is equilateral, let its side be 10. According to the calculation above, the radius of circle O is 10. The radius of 2nd circle is 5. Circle X is within another similar triangle (equilateral also) of CZB, and its vertex is pointing at C. Note that the base of this similar triangle is a perpendicular tangent to circle X and circle O. Its height is 10, which is the radius of circle O. The side of this similar/equilateral (bigger than CZB) triangle is, 10/sin 60=S/sin 90, thus S=11.547. Circle X is inside this equilateral triangle; its radius is the height of the triangle (10 divided by 3). Because perpendicular lines from each side meeting at a point adds up to give the height of the triangle (1/2 x B x H1) + (1/2 x B x H2 ) + (1/2 x B x H3)=1/2 x B x H, so H1 + H2 + H3=H. Therefore, the radius of circle X is 10/3. If the line-joining center of circle X to C is perpendicular to AB, the figure that pointed at the center of the 2nd circle, the center of circle X and point C must be a right angle triangle. The height of this triangle is, 10-10/3. Its tangent is 5+10/3 and the base is 5. Applying Pythagoras Theorem to see if it is a right angle triangle, we have, (10-10/3)^2 + 5^2=69.44 And (5+10/3)^2=69.44 It is a right angle triangle. Therefore the line joining the center of circle X to point C is perpendicular to AB.
Claudia Baiocchi: Refering to:Let us draw just the first two circles; R1, R2 will denote theyr radius; C1, C2 theyr centers. We ask for a third circle tangent to both and with center C3 on the perpendicular in C to AC. Let R3 be the third radius, and let D be the distance of its center to C. As obvious from the enclosed picture, we have: (R2+R3)^2=D^2+R2^2; (R1-R3)^2=D^2+(2R2-R1)^2 and, by substraction, we can solve linearly in R3, thus getting: R3=2R2(R1-R2)/(R1+R2); D^2=8R1(R2-R2)R2^2/(R1+R2)^2 In particular the ratio R3/D (which is the sinus of the angle in C between the tangent line to the third circle and the vertical line) is the sqare root of (R1-R2)/R1; an easy check shows that this corresponds exactly to the angle needed to constuct the triangle.
John Hewson Let O be the centre of the circle O and the origin of a coordinate system with AB as x-axis. Let S be the circle with diameter AC and let S have centre D. Let the radius of O be 1, the radius of S be a<1, and the radius of X be r. Let (p,q) be the centre of X. Then D is (- (1 - a) , 0) and C is (2a - 1 , 0). Let N be the mid-point of the base CB of the isosceles triangle and V its vertex. Then N is (a , 0) and V is (a , h) where h^2 = 1 - a^2 X touches S externally which implies that the sum of the radii of X and S = the distance between their centres. ie (r + a )^2 = (p + 1 - a)^2 + q^2 .... (1) X touches the circle O internally which implies that the difference of the radii of X and O = the distance between their centres. ie (1 - r)^2 = p^2 + q^2 .... (2) X touches side VC which implies that the perpendicular distance form the centre of X to VC = the radius of X. Now the equation of VC is h*x - (1 - a)*y + h*(1 - 2a) = 0, and the distance of (p , q) from VC is: r = [-h*p + (1 - a)*q - h*(1 - 2a)]/sqrt(h^2 + (1 - a)^2). .... (3) It can be verified by direct substitution that the three equations (1), (2), and (3) have solutions for p, q, r as follows: p = 2a - 1 q^2 = 8(a^2)*(1 - a)/(1 + a)^2 r = 2a*(1 - a)/(1 + a) But the coordinates of C are (2a - 1 , 0). Thus the x-coordinates of (p , q), the centre of X, and of C are equal (both 2a - 1) and the line from C to the centre of X is perpendicular to the x-axis AB.
Jozef Hanenberg Given the circle c1 with diameter AB, center M1 and radius R. Given the circle c2 with diameter AC (C on AB), center M2 and radius r. Given the isosceles triangle BCD with D on c1. Let E be the middle of BC. Given line k through C with k perpendicular to AB. Prove that the center M3 of the circle c3, that is tangent to the circles c1, c2 and to the triangle BCD, lies on line k. We turn the problem around: we create circle c3 in such a way that M3 lies on k and c3 is tangent to c1 and c2. We then prove that BD is a tangent to this circle. Because there can be at most one circle that is tangent to all three, this must be that circle and it follows that CM3 must be perpendicular to AB. By shifting M3 from C upwards over line k we see that there is only one position of M3 on k in which M3 is the center of a circle that is tangent to both c1 and c2: name this circle c3 and let s be the radius. Look at the triangle M1M2M3, formed by the three centers. M1M2 = R - r, M2M3 = r + s, M1M3 = R - s. Because C is on M1M2 and CM3 is perpendicular to M1M2 we have two right-angled triangles M1CM3 and M2CM3 with CM2 = r and CM1 = Abs(R - 2r). Let CM3 be x. With Pythagoras we find i) (r + s)^2 = r^2 + x^2 and ii) (R - s)^2 = (R - 2r)^2 + x^2. i) leads to iii) x = Sqrt(2rs +s^2) and substituting x^2 = 2rs +s^2 in ii) and isolating s gives us iv) s = 2r(R-r) / (R+r) Now draw a line through C that is tangent on c3: let P be the point where this line touches c3. (P of course lying on the same side of CM3 as point D.) The triangle CPM3 is right-angled, because radius M3P is perpendicular to tangent CP. Using iii) and iv) we find the following expression: sin PCM3 = PM3 / CM3 = s / x = s / Sqrt(2rs + s^2) = Sqrt(s) / Sqrt(2r+s) = Sqrt(2r(R-r)/(R+r)) / Sqrt(2r + 2r(R-r)/(R+r)) which simplifies to v) sin PCM3 = Sqrt((R-r)/(2R)) Now let's look at triangle CDE. CE = BC/2 = R-r. We calculate DE in triangle DEM1. EM1 = M1B - BE = R - (R-r) = r. M1D = R and so we find DE = Sqrt(R^2 - r^2). With Pythagoras we find CD^2 = CE^2 + DE^2 = (R-r)^2 + R^2 -r^2 = 2R(R-r) and CD = Sqrt (2R(R-r)) Because triangle CDE is right-angled we find sin EDC = CE / CD = (R-r) / Sqrt (2R(R-r)). This can be rewritten as vi) sin EDC = Sqrt ((R-r)/(2R)). From v) and vi) we may conclude that the angles PCM3 and EDC are equal and because the lines CM3 and ED are parallel we can see that the lines CD and CP are in fact one and the same line. So CD is tangent on c3. QED.
Radu Casian Ionescu Consider a circle O with a diameter AB and O center,R radius. Draw a second circle with diameter AC and D center,r radius, such that C is on AB in circle O. Draw a third circle (X) and E center, x radius, tangent to the first two figures and such that the line from C to the center of circle X is perpendicular to AB. In triangle OEC : EC^2=(R-x)^2 - (2r-R)^2 (1) In triangle DEC : EC^2=(r+x)^2 - r^2 (2) (1) and (2) ===>x= (2r(R-r))/(R+r) and EC=2sqrt(rR/(R+r)) Let be F such that CF is tangent to circle (X). In triangle EF/EC=sqrt((R-r)/2R) (3) Draw an isosceles triangle with base CB and third vertex G on circle O.Let be H the projection of G to AB. CH=HB=R-r Triangle HGB and GAB are simili==> HB/GB=GB/AB ==> GB^2=2r(R-r)=CG^2 CH/CG=sqrt((R-r)/2R) (4) (3) and (4) ==> Triangle CEF and GCH are simili (5) EC and GH are parallel (6) (5) and (6) ==> CF and CG are the same ==> F is on CG
Allen Druze Let point x be the center of circle x. Let the top of the isosceles triangle be point E. From point C draw a line that is tangent to circle x at F and extend thru point F to point D such that CD is equal to CE. Circumscribe a circle about triangle CDE. Angles CDE and BCE are both measured by one half of arc CE, therefore angle CDE = angle BCE and since triangle CDG is isosceles( by construction) then angle DEC = angle BEC and triangle CDG is congruent to triangle BCE(a.s.a), hence BCDE is a parallelogram. Let point G lie on line CE where CE is tangent to circle x. Draw lines XF and XG. Right triangles XFC and XGC are congruent(s.s.s), then angles FCX and GCX are equal and XC bisects angle DCE . Extend XC to base DE as XC is not only the angle bisector but is also the altitude of triangle CDE, which means it is also perpendicular to base DE , hence is also perpendicular to diameter AB because DE was proven to be parallel to AB.