A Domino Overhang
Let the length of a domino be 1. On the edge of a table, a single
domino can extend out a distance of 1/2 before being unbalanced. A stack
of two dominos can extend out a distance of 3/4. How large of an overhang
can you create with 5? 10? N? How many dominos are needed before the top
domino is one full horizontal length away from the edge of the table, for a full overhang
length of 2? Each domino must be placed in the same orientation (don't
rotate the dominos or stand them on end.)
Extension: Does it make a difference how far the overhang reaches if you can place dominos on top as extra weight?
For example, the same 2-domino distance of 3/4 can be reached when the bottom
domino extends out and the top domino is placed back as ballast:
====
====
Table----
Source: Past puzzle experience. This can also be done with playing cards.
Update October 22, 2007: Some new sources on the web analyze this same
problem:Maximum Overhang:
http://arxiv.org/abs/0707.0093
Overhang:
http://arxiv.org/abs/0710.2357
Solutions were received from Philippe Fondanaiche, Alan O'Donnell, and Alan
Zimmermann. I'm still wondering if a more complete analysis of the
problem with ballast exists.
Alan O'Donnell sent links to other sources:
I think this article answers all the questions in your POTW:
http://mathforum.org/advanced/robertd/harmonic.html
also in layman's terms:
http://www.naturalmath.com/paradoxes.html#16
Summary of results from Alan Zimmermann:
With n dominos the maximum overhang is (1 + 1/2 + 1/3 + … + 1/n) / 2.
Some specific values are as follows:
n Maximum Overhang
--- -------------------------------
1
1/2 = 0.5
2
3/4 = 0.75
3
11/12 = 0.916666666666667
4
25/24 = 1.04166666666667
5
137/120 = 1.14166666666667
10 7381 /
5040 = 1.46448412698413
31
145387128648679 / 72201776446800 = 2.01362259771826
31 is the smallest n that provides an overhang of at least 2.
Philippe's sent some good pictures in his solution below. [I believe
there is a slight error in his second half and have asked him for modifications
7/28/03. -KD]
Let the top domino numbered 1. Let O the origin of the axis Ox at the right
end of this domino with Ox pointed towards the left.
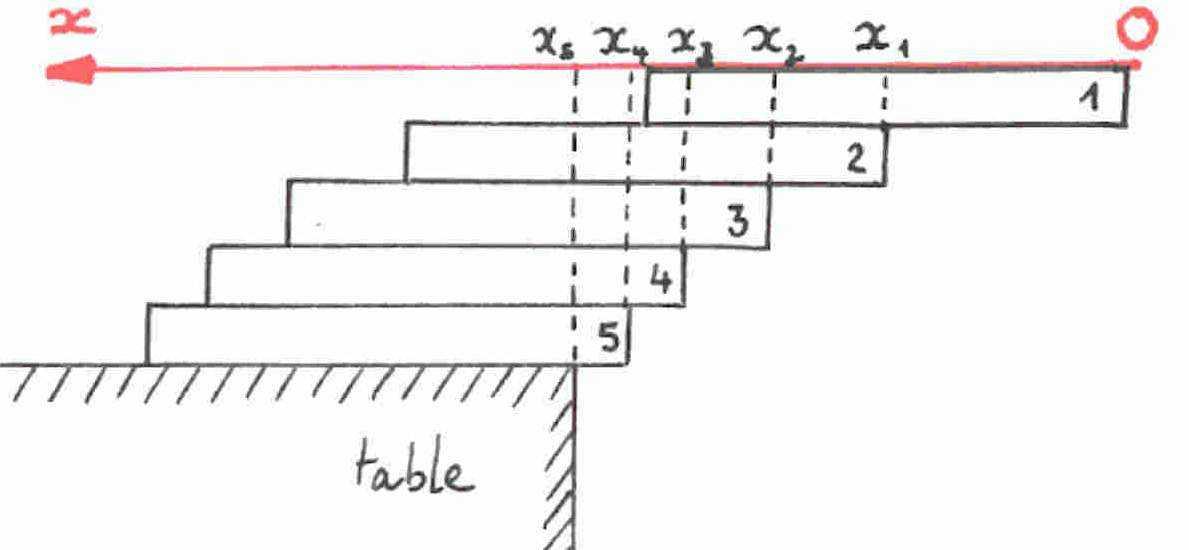
The domino 1 remains unbalanced iff the centre of gravity (abscissa x_1) is
above the domino 2, put just below.
Therefore, we can move forward the domino 2 of 0.5. The center of gravity of
the group made of the two dominoes 1 and 2 is of abscissa x_2 = [ x_1 + (x_1 +
0.5) ] / 2 = x_1 + 0.5 / 2.
Then we can move the domino 3 of 0.5 / 2 =0.25. The center of gravity of the
group made of the dominoes 1,2 and 3 is of abscissa x_3 = [2*x_2+(x_2+0.5)] /
3=x_2 + 0.5 / 3.
So the domino 4 can be moved of 0.5 / 3
etc....
More generally, x_n = [ (n-1)*x_(n-1) + (x_(n-1) + 0.5) ] / n = x_(n-1) + 0.5 /
n and the domino can be moved of 0.5 / n as compared to the domino n-1.
As the sum [1/n] for n=1 through infinity is divergent, if we are patient with
many, many dominoes at our disposal, we can build an arch as long as
possible.
For n=5, the overhang is equal to 0.5*sum[1/n] for n=1 to 5 = 1,14166..
For n=10, the overhang is equal to 1,464484....
The numbers n such that the overhang are at least equal respectively to 2 and 3
are
n=31 with x_31 = 2,0136...and n=227 with x_227 = 3,00218..
If dominoes are placed back as ballast, it is possible to "speed" the
building of the arch.
Hereafter an example with 9 dominoes used as ballast and the domino numbered 6
at the
end of the arch which shows an overhang of 1,75 greater than the overhang
obtained
previously and equal to 1,55516..
On
the diagram, it appears that formally the dominoes 6 and 10 will fall off of
domino 12.
In order to avoid that, it is enough to slide very slightly the domino 9 of a
length “epsilonn”
towards the right so that the domino 10 is maintained. The domino 8 is
moved of the same
length “epsilonn” towards the left and the other dominoes 7,5,4,3,2,1 keep
the same
position so that the center of gravity of the ballast is unchanged.
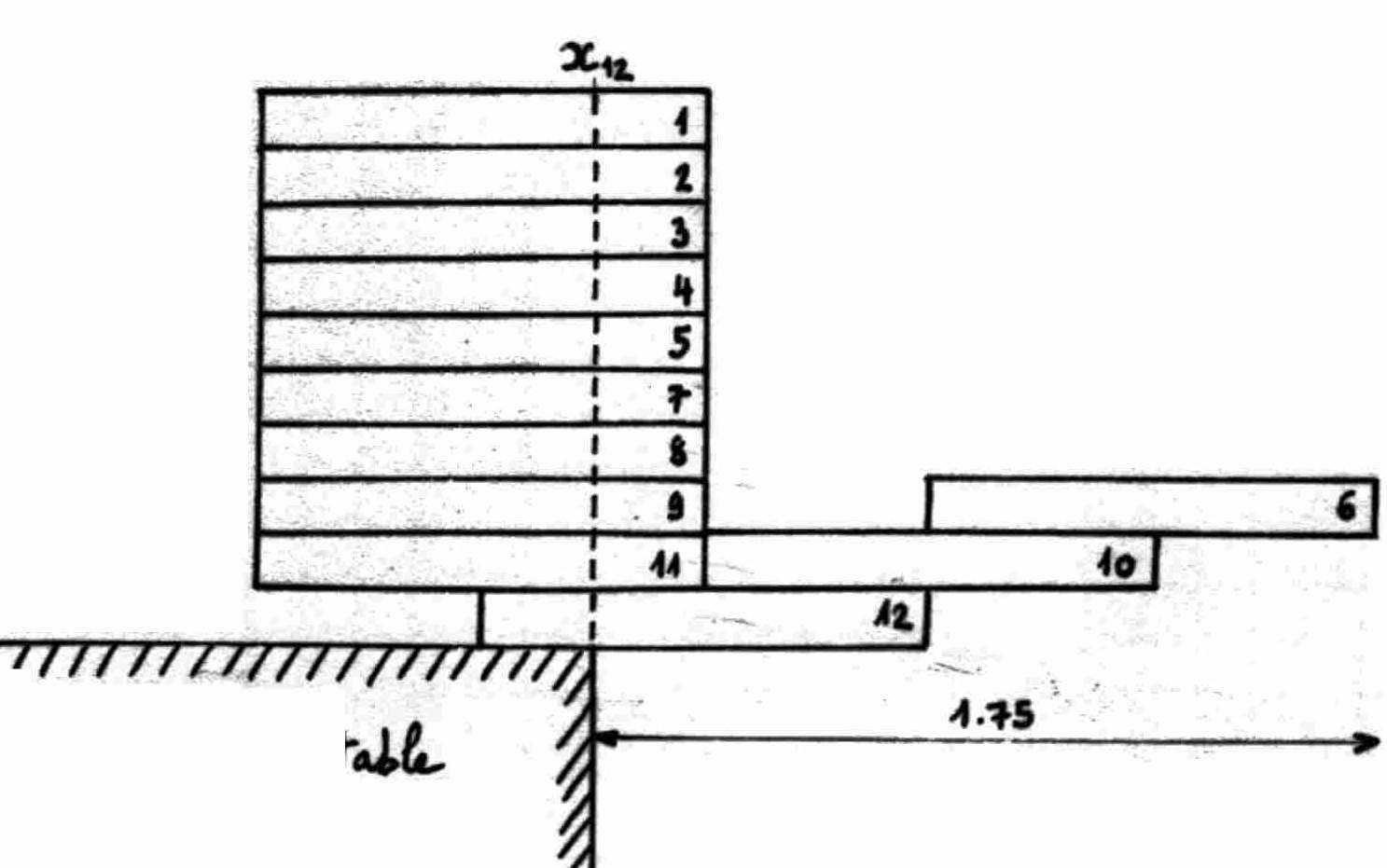
The process can be easily extended with the domino numbered 13 on the domino
numbered 6
(as 6 on 10) and 7 new dominoes piled on the ballast, etc...
Update 7/29/03: Joe DeVincentis sent this little note on ballast:
On the domino stacking problem with ballast last week, if you arrange
dominoes in a triangular pattern, you can get an overhang of n/2 for
(n^2 + n)/2 dominoes. It's probably possible to do better, as some of
the dominoes don't seem strictly necessary, but it far exceeds the
harmonic sum overhang achieved without ballast.
aabbccddee
ffgghhii
jjkkll
mmnn
oo
======
| |
Update 12/19/03: Jeremy Galvagni tried to build this structure and found:
jjkkll
mmnn
oo
======
This cannot be made because jj/mm and ll/nn push up too hard on kk,
unsettling the system.
Mail to Ken

