A Broken Clock Face
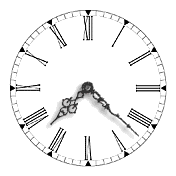
|
|
Break the Roman-numeral clock face into four pieces, such that the sum of the
resulting numbers on each piece is the same. All numerals can be read from
the center of the clock face.
|
Source: Henry Ernest Dudeny's 536 Curious Problems & Puzzles, #49.
Solutions were received from Nick McGrath, Al Zimmermann, David Bachtel, Ravi
Subramanian, Andrew Jackson, Toby Gottfried, Denis Borris, Joseph DeVincentis,
Radu Ionescu, Alan O'Donnell, and Carlos Rivera. Everyone found that
since the total of the clock-face numbers in 78, not divisible by. The IX
must be broken to make the new total 80, and each of the four pieces will sum
to 20. After this there are a number of solutions (some are below). [Denis
Borris also wanted it known that if the piece with XI ends up inverted, then
the new total is 76, and each of the four pieces can be made to sum to 19,
instead.]
Various solutions:
From Nick McGrath:
- Piece containing the X from the IX (9)
and the X (10) Total 20.
- Piece containing the I from IX (9);
the XI (11) and the VIII(8). Total 20.
- Piece containing the XII (12), I
(1), II (2), III (3) and II from the IIII(4) . Total 20.
- Piece containing the other II from
IIII(4), V (5), VI (6) and VII(7). Total 20.
From Joseph DeVincentis:
- X, and the X from IX.
- VIII, I from IX, and XI
- VII, XII, and I
- II, III, IIII, V, and VI
From Carlos Rivera:
- …..I, XII, I,II,III,I…..
- ....III, V, VI, VI...
- ....X, X
- ....I, VIII, I… X….
Denis Borris' 19's:
- XII I II III I(from IIII)
- III(from IIII) V VI V(from VII)
- II(from VII) VIII IX
- X XI (read right to left; the broken piece "landed" as IX X!)
Update 9/23/03. Oliver Stone sent this extension:
If the clock broke so that the numbers I, II, III,
and/or IIII were split widthwise, you would have two copies of each. The
the totals would be 84 (IIII didn't split) or 88 (IIII split), and there are
solutions for each:
XII + outside half of I, II, III, and IIII = 22
X, XI, + inside half of I = 22
VIII, IX, + inside half of II, III = 22
V, VI, VII + inside half of IIII = 22
Also,
X, XI = 21
IX + XII = 21
VII, VIII, +inside half of I, II , III = 21
IIII, V, VI, + outside half of I, II, III = 21
Thought you might like this different way of
splitting the numbers. You can't split the X's this way because all the
numbers must be able to be read from the center of the clock, but the I's are
fair game.
Mail to Ken

