Let a square ABCD.
The first natural method to divide this square in right triangles is to try to find:
1) a point E on AB such that ADE and BCE are right triangles and the triangle CED is split in two right
triangles with the height drawn from C (or from D). Let AB=n and AE=a with a and n integers a<>n/2.
We have to find a and n such that a^2+n^2 is a square and (n-a)^2+n^2 is also a square.
There is no solution for n<5000 and probably whatever n.
or
2) a point M within the square such that MA,MB,MC and MD are integers. If this point exists, it is easy
to divide the square in 4 pairs of identical right triangles and to subdivide one triangle of each pair into two
unique right triangles.
Such a point M does not exist....
So we have considered many other approaches. Only one of them provides a significant number of possible
solutions and consists of finding 4 points E,F,G,H respectively on AB,BC,CD and DE such that the triangles
AEH, BEF, CFG and DGH are Pythagorean and the diagonal EG or HF is an integer (see the diagram hereafter)
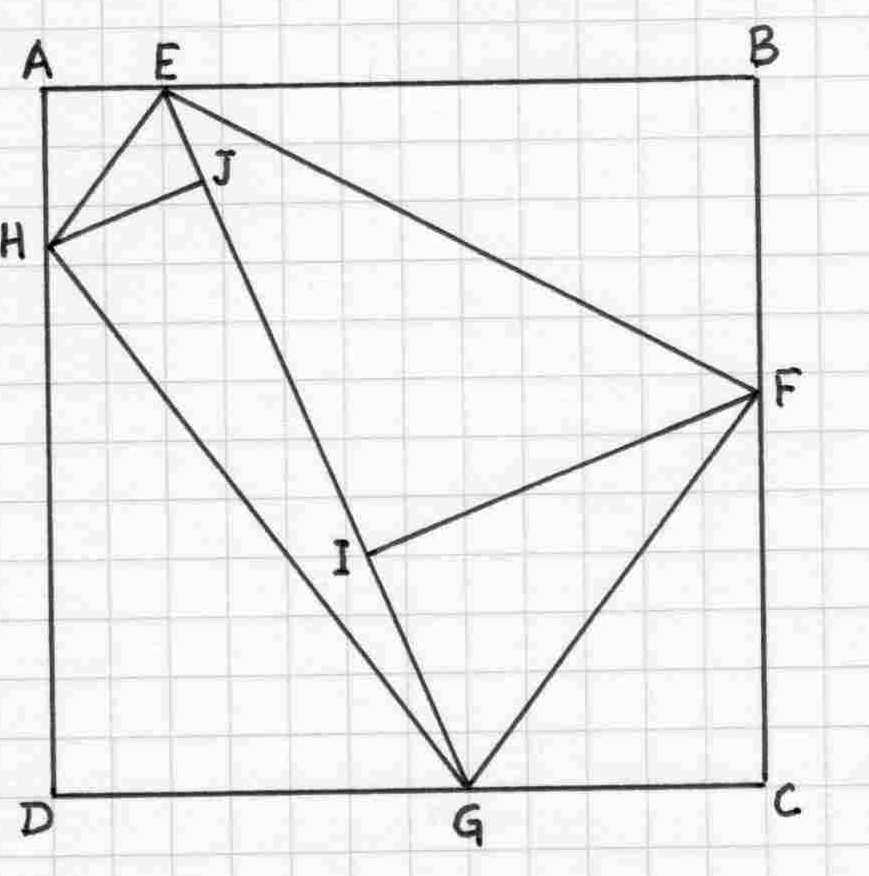
With a square of side equal to 468, we obtain 8 eight right triangles with the following measures:
The sides of the right triangles are a1<a2<a3.
If the ratios a1/a2 are the same, the corresponding triangles are similar.
triangles a1 a2 a3 a1/a2
AEH 78 104 130 0,75
BEF 208 390 442 0,5333..
CFG 195 260 325 0,6
DGH 273 364 455 0,75
EFI 280 342 442 0,81871...
FGI 165 280 325 0,589285...
EHJ 66 112 130 0,589285...
GHJ 112 441 455 0,253968..
Question 2
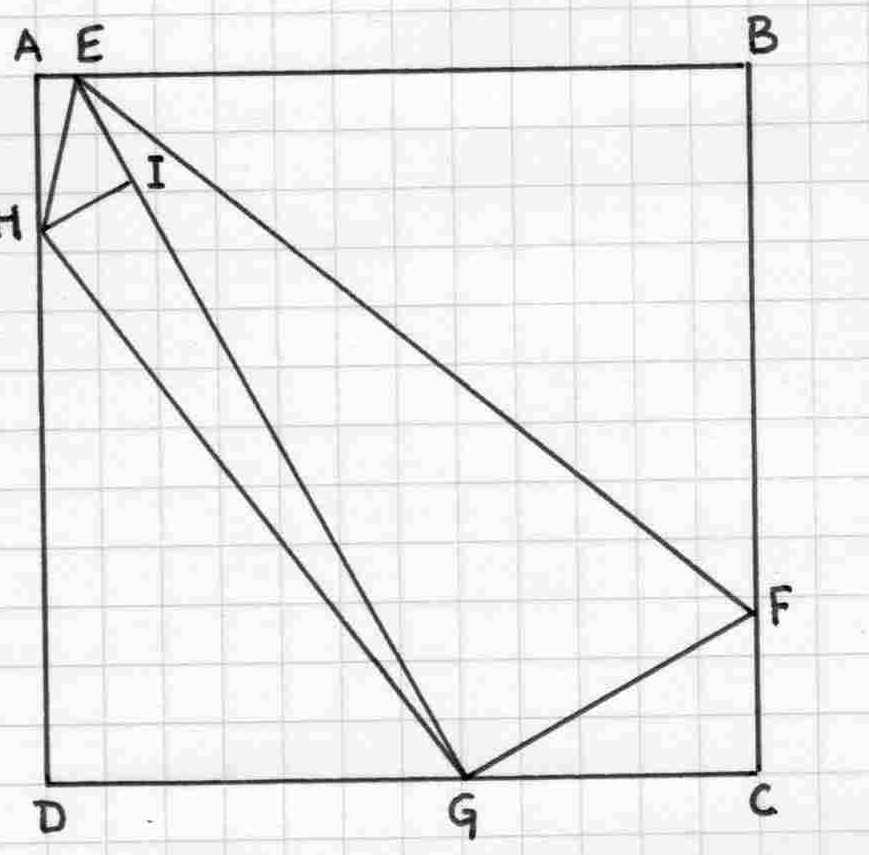
With the same approach as above but with the constraint that all the ratios a1/a2 are different, we get
a square of length n=3060 which can be divided into 7 right triangles as EGF is already a right triangle.
triangles a1 a2 a3 a1/a2
AEH 153 680 697 0,225
BEF 2380 2907 3757 0,81871..
CFG 680 1275 1445 0,5333..
DGH 1785 2380 2975 0,75
EHI 455 528 697 0,861742...
EFG 1445 3468 3757 0,41666..
GHI 455 2940 2975 0,154761..
We can take the opportunity to look for a square divided into a minimum of right triangles.
In this case, the pattern is defined hereafter with a point E on AB and a point F on AD. We succeed
to divide the square into only 5 right triangles. The side of the square is n=9000.

triangles a1 a2 a3 a1/a2
AEF 3400 6375 7225 0,53333...
BEC 5600 9000 10600 0,62222...
CDF 2625 9000 9375 0,291666..
EFG 1479 7072 7225 0,2091346...
CFG 7072 7896 10600 0,895643...
Question 3
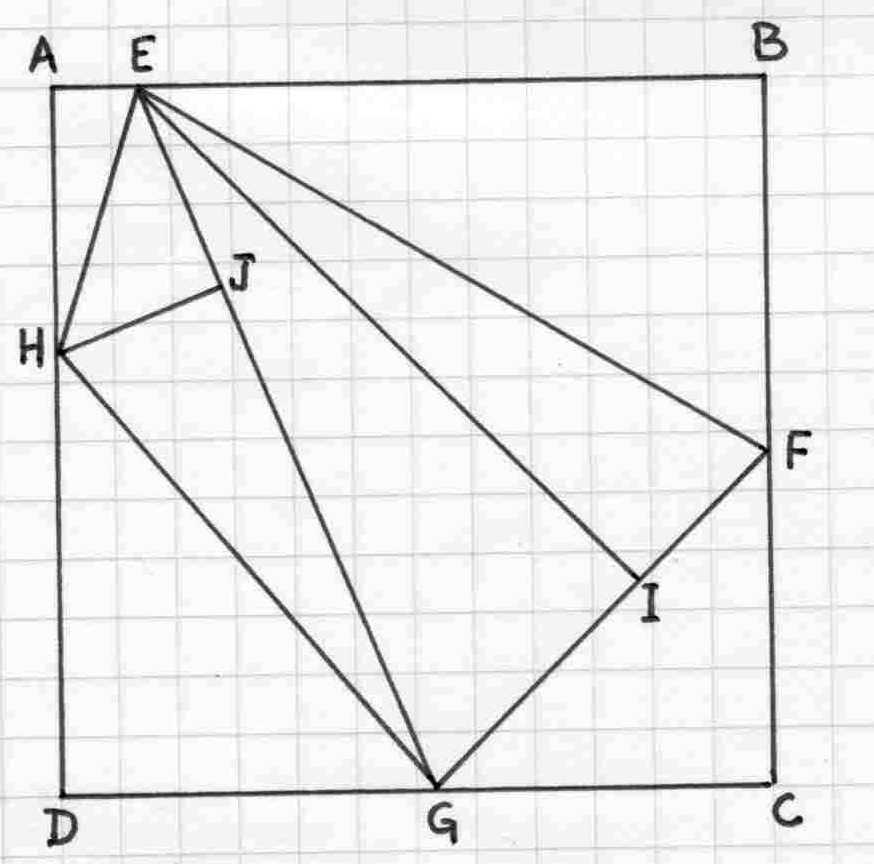
We use again the same approach as in Q1 and Q2 and we get a square of side equal to 3276
divided into 8 non-similar right triangles with the following diagram and measures:
triangles a1 a2 a3 a1/a2
AEH 364 1248 1300 0,291666..
BEF 1716 2912 3380 0,589285..
CFG 1547 1560 2197 0,991666...
DGH 1729 2028 2665 0,852564....
EHJ 816 1012 1300 0,806324...
EFI 832 3276 3380 0,253968...
EGI 1365 3276 3549 0,416666...
GHJ 816 2537 2665 0,321639....