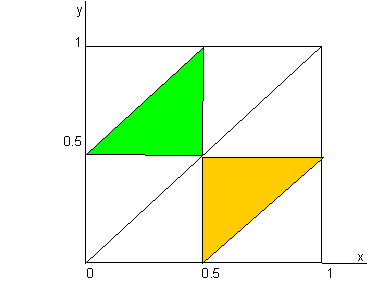
Then the odds the three pieces make a triangle are given by the ratio of the sum of the areas of the green and yellow triangles to the area of the square, that is to say: 1/4=0.25
Source: Past Puzzle Experience.
Q1
Let
X and Y the abscissas of the first and the second points chosen at random on
the stick. X and Y are two random and independent variables uniformly
distributed on the square [0,1].
If
X>Y, then three pieces are Y, X-Y, 1-X long and can make a triangle if X and
Y belong to the yellow triangle defined in the following diagram. If X<Y,
the three sticks are X, Y-X and 1-Y long and make a triangle if X and Y belong
to the green triangle.
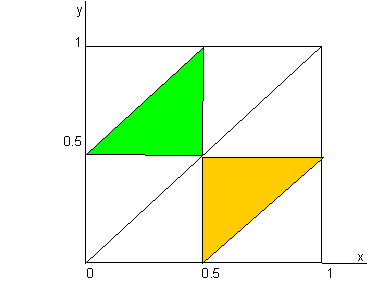
Then the odds the three
pieces make a triangle are given
by the ratio of the sum of the areas of the green and yellow triangles to the
area of the square, that is to say: 1/4=0.25
Q2
In
this case, the second point is chosen at random on the stick X or on the stick
1-X. As one of the two sticks is again chosen at random (1/2 for each of them)
and as the probability laws of X and of 1-X are strictly the same, we can limit
the analysis to the stick X.
Y is
uniformly distributed on [0,x]. So the probability law of (X,Y) is defined by
f(x,y)=1/x within the right isosceles triangle OAB.
As
above, the three pieces make a triangle if X and Y are in the red triangle:
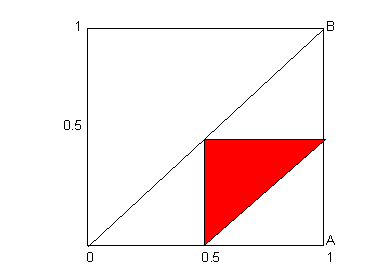
Then the odds the three
pieces make a triangle is sum[sum[dx*dy/x]] on the red triangle = Ln[2] – 0.5
= 0.193147....