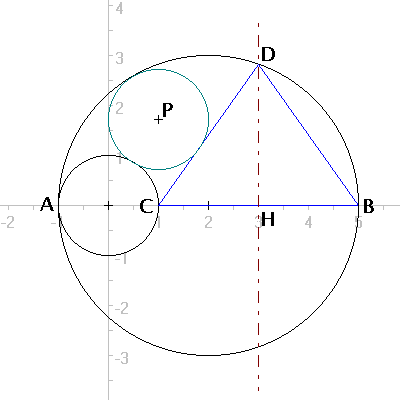
AC = AB/3
Source: Related to past problem.
Everyone found that the radii of the small circles is exactly 1/3 of the large circle. Radu Ionescu' solution builds upon the previous problem:
If we look at Radu Casian Ionescu's solution of "A Sangaku
Problem":
" x=(2r(R-r))/(R+r) " take r=x ==> r=R/3 ==> AC=2R/3
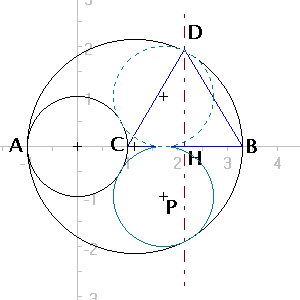
Alessandro Fogliati found an additional solution that meets the stated problem requirements. His two soltutions are here:
AC = AB/3 |
AC=AB*3/(3+sqrt(10)) [provided I did my math right - KD].
|