Dots and Squares
In the classic game, two players alternate turns, adding a line between two
dots. In a turn, if a player creates a unit square, they claim that square
for their score and must then add another line (if two squares are created at
once, they still add only a single line.) When a player places a line and
no square is created, the next player takes a turn. In each puzzle below,
it is Player 1's turn.
 | |
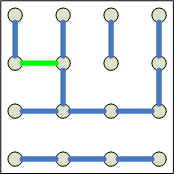
1. The game has reached the state to the left. Only one line will
guarantee Player 1 the win. Which one? |
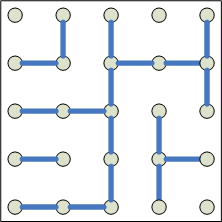 | |
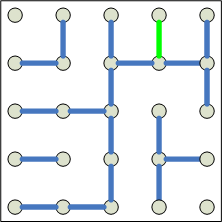
2. The game has reached the state to the left. Player 1 can guarantee a
win with what strategy? |
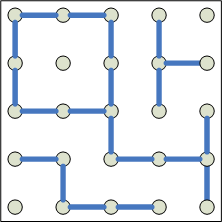 | |
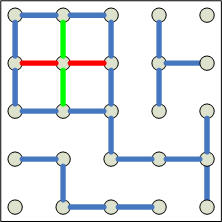
3. The game has reached the state to the left. Player 2 can guarantee a
win with what strategy? |
Source: Original.
Solutions were received from
Alan O'Donnell, Kirk Bresniker, Yaacov Yoseph Weiss, Dan Chirica, and David
Stignant. Below is a summary of the answers, followed by Yaacov's
summary of the solutions.For #1 and #2, player 1 will lead to a win by playing the green line of the
2-square section. If he plays either end of the 2-square section,
player 2 could lead to a win by playing the opposite end. For #3,
player 2 can win by splitting the square when player 1 plays there (play to
complete the green or red line.)
Yaacov's summary:
The key nonobvious strategy is that when completing a
block, you should often leave the last 2 squares for
the other player, forcing him to offer another block.
A corollary is that a block of 2 should be offered in
such a way that the opponent must take, and cannot
offer it back. (It is a controlling option, if it is
better for opponent to take, he will take anyway.)
1:
Thus in the first case, the key is to offer
the pair, without allowing a counteroffer. Then give 2
squares from the block the opponent chooses, and take
the whole complete block. Player1 wins 5-4. [KD: Yaacov also pointed out
that this problem can be solved through symmetry - the highlighted line is
the only unique good move.]
2:
The single blocks in the corner are traded, and then
the key is (as before) offer the pair on the top right
without allowing a counteroffer. Opponent gets one of
single squares, the pair, and 2 pairs from the 3
blocks. Total of 7/16. player 1 wins. Note that player
1 can start by offering a singleton. Any response from
2 gets the same response it would get later, except
that if p2 offers the pair, (even allowing a
counteroffer,) p1 takes and offers the second single.
3:
Again the singles in the corners get traded. The idea
is the same also here. If p1 first offers the 5s, p2 gets 1+3+3+4=11. If p1
offers the 4, p2 is forced to not take it at all, leaving those 4 for p1. p2
compensates with taking a complete set of 5 later, totalling 1+3+5=9.
Mail to Ken