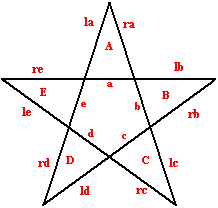
THE PROBLEM Following Ken Duisenberg (LINK TO MODIFY WHEN THE PROBLEM WILL BE MOVED INTO ARCHIVES) we want to assign the numbers 1-15 to each of the line segments on a 5-pointed star such that every line and every small triangle has the same sum.

NOTATIONS We denote by a, b, c, d, e the values we will put on the bases of the triangles A, B, C, D, E respectively; using "l" for left and "r" for right, the corresponding sides will be denoted by la,ra; lb,rb and so on.
If S denotes the common value of the 10 sums, taking into account that any value appears into two sums, we must have 10*S=2*(1+2+...+15); thus S=24. Remark that the discussion could be somewhat shortened by using, instead of the numbers (1,...,15), the numbers (-7,...,+7); say substracting 8 to each entry. In particular, the common value of the sums becomes 0.

REDUCTION OF CASES A quite obvious reduction of cases is given by the remark that rotations and/on symmetries transform solutions into solutions; in particular a rotation allows us to assume a < b, c, d, e; then, possibly using a symmetry with respect the base of the triangle A, we can assume b < e. The following two properties are somewhat less obvious:

1. any solution has a "twin-solution" obtained by swapping 5 couples of values: ra<-->lb, rb<-->lc,...,re<-->la. In particular we can assume la<rb
2. any solution has a "dual-solution" obtained by replacing each value X with 16-X; under duality, the sum SB=a+b+c+d+e changes into 80-SB; thus we can confine ourselves to assume SB ≤ 40: solutions with SB < 40 will surely differ from the corresponding dual, while solutions with SB = 40 need a further check: they could be "auto-dual" say coincide (after a rotation and/or a symmetry) with the dual one.

STRATEGY A possible strategy could be to fix 6 elements (suitably choosen, e.g. the bases a, b, c, d, e and the side la); then imposing the value 24 to the 10 sums we get a unique set of 15 values, that we will obviously accept only if the resulting 15-tuple coincide with the set (1,...,15). Of course this is too expansive, but the previous remarks can shorten the work:

• we can let a vary only between 1 and 6 because a+(a+1)+(a+2)+(a+3)+(a+4) ≤ 40;
• then b can vary between a+1 and 14 and e between b+1 and 15;
• c,d can vary between a+1 and 15;
• la can vary from 1 and 15; but we can also impose 2la < 24-a+b-c+d-e because otherwise we would end up with la > re.

RESULTS The resulting program (written in any language faster than JavaScript!) will output 6 solutions with SB < 40 and 3 solutions (all autodual) with SB = 40. In particular, if we only search for solutions modulo rotations and/or symmetry, the problem has 30 solutions.