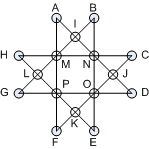
Place the numbers 1-16 in locations A-P such that each line has the same sum.
Solve for all possible sums.
Source: Original (though likely elsewhere, too...)
Let S the common sum to the eight lines abd a,b,c,d,e,f,...the values in
locations A,B,C,D,E,F,...
We have 8 relations such as a + m + p + f = S, a + i + n + j + d = S, b
+ n + o + e = S, etc...
By addition of these relations, we can infer 2*(a + b + c + d +....) + m
+ n + o + p = 8S.
As a + b + c + d +....+ o + p = 17*16/2 = 136, we get S = 34 + (m + n +
o + p )/8. That means that the sum of the 4 terms m, n, o and
p must be a multiple of 8.
On the other hand by eliminating successively a,b,c,d...in the eight
relations, we get a relation between the remaining variables i, j, k, l,
m, n, o and p : 2*( i + j + k + l) = m + n + o + p.
As the minimum value of i + j + k + l is 1 + 2 + 3 + 4 = 10, the minimum
value of m + n + o + p is >=2*10 = 20. The fisrt number >= 20 divisible
by 8 is 24. So the minimum value of S is 37.
At last the maximum value of of m + n + o + p is 16 + 15 + 14 + 13 = 58.
The first number <=58 which is divisible by 8 is 56. So the
maximum value of S is 41.
As a conclusion the possible values of S are 37, 38, 39, 40 and
41.
There exist many solutions for each of these values.
Hereafter, one solution is
given as an example for each possible value of S.
|
Sum = 37 |
|
|
|
|
|
|
|
|
|
|
Sum = 38 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
15 |
|
|
|
|
|
|
|
|
|
|
14 |
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
12 |
|
4 |
|
5 |
|
16 |
|
37 |
|
|
|
|
16 |
|
2 |
|
7 |
|
13 |
|
38 |
|
|
|
|
|
|
6 |
|
|
|
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
3 |
|
|
|
|
|
|
|
|
9 |
|
8 |
|
7 |
|
13 |
|
37 |
|
|
|
|
9 |
|
12 |
|
11 |
|
6 |
|
38 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
37 |
|
|
|
11 |
|
10 |
|
|
|
37 |
|
|
38 |
|
|
|
10 |
|
5 |
|
|
|
38 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
37 |
|
37 |
|
37 |
|
37 |
|
|
|
|
|
|
38 |
|
38 |
|
38 |
|
38 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sum = 39 |
|
|
|
|
|
|
|
|
|
|
|
Sum = 40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
16 |
|
|
|
|
|
|
|
|
|
|
|
11 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
13 |
|
4 |
|
14 |
|
8 |
|
39 |
|
|
|
|
|
7 |
|
4 |
|
15 |
|
14 |
|
40 |
|
|
|
|
|
6 |
|
|
|
10 |
|
|
|
|
|
|
|
|
|
12 |
|
|
|
1 |
|
|
|
|
|
|
|
12 |
|
15 |
|
7 |
|
5 |
|
39 |
|
|
|
|
|
6 |
|
16 |
|
13 |
|
5 |
|
40 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
39 |
|
|
|
11 |
|
2 |
|
|
|
39 |
|
|
|
40 |
|
|
|
9 |
|
2 |
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
39 |
|
39 |
|
39 |
|
39 |
|
|
|
|
|
|
|
40 |
|
40 |
|
40 |
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sum = 41 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
11 |
|
14 |
|
12 |
|
41 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
16 |
|
15 |
|
2 |
|
41 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41 |
|
|
|
1 |
|
5 |
|
|
|
41 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
41 |
|
41 |
|
41 |
|
41 |
|
|
|
|
|
|
|
|
|
|
|
|