Solution to Problem 1: AB = 5 and PD = sqrt(17) with P inside the square, AB = 1 and PD = sqrt(17) with P outside the square. Problem 2: PD = 11 and AB = sqrt((539-98*sqrt(17))/106) + sqrt((8171-98*sqrt(17))/106) with P inside the square. PD = 11 and AB = sqrt((4655-98*sqrt(17))/106) - sqrt((415-98*sqrt(17))/106)) with P outside the square.[These are the correct values (though I have a little simpler form for the last numbers.) -KD]
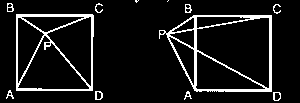
Drawing perpendicular lines through point p (parallel to the sides) you
receive 4 rectangles, with PB, PC, PA, and PD as the diagonals. I
labelled the shorter segments on the sides (made from the perpendicular
lines above) x, y, z, and w so that:
x^2 + y^2 = PB^2 (x^2 + y^2 = 9),
y^2 + w^2 = PC^2 (y^2 + w^2 = 10),
x^2 + z^2 = PA^2 (x^2 + z^2 = 16).
By manipulating these equations (or solving them with a matrix) one will
find that:
z^2 + w^2 = 17.
Therefore PD^2 = 17, PD = sqrt{17}.
With the other situation, z^2 + w^2 = 121, therefore PD = 11.
At last, I solved this problem:
Let AP=a, BP=b ,CP=c and DP=d. AB=x.
It is easy to see that a^2 + c^2 = b^2 + d^2, but I don't need this
result in my proof.
Let angle(ABP)= Beta, so angle(CBP)=90-Beta.
Looking at Triangle ABP and the cosine-rule:
(1) a^2 = b^2 + x^2 -2*b*x*cos(Beta)
Looking at Triangle CBP and the cosine-rule:
(2) c^2 = b^2 + x^2 -2*b*x*cos(90-Beta)
Because cos(90-Beta) = sin(Beta):
(3) c^2 = b^2 + x^2 -2*b*x*sin(Beta)
Rewrite (1) and (3):
(4) 2*b*x*cos(Beta) = b^2 - a^2 + x^2
(5) 2*b*x*sin(Beta) = b^2 - c^2 + x^2
And thus:
(6) 4*b^2*x^2*cos^2(Beta) = (b^2 - a^2 + x^2)^2
(7) 4*b^2*x^2*sin^2(Beta) = (b^2 - c^2 + x^2)^2
------------------------------------------- +
(8) 4*b^2*x^2 = (b^2 - a^2 + x^2)^2 + (b^2 - c^2 + x^2)^2
(Because cos^2 + sin^2 = 1 for each possible angle)
So formula (8) is a quadratic formula in x^2
Rewriting this formula results in:
x =
0.5*sqrt(2*a^2+2*c^2+sqrt((2*a^2+2*c^2)^2-8*(b^2-a^2)^2-8*(b^2-c^2)^2))
(If P is inside the square)
AND
x =
0.5*sqrt(2*a^2+2*c^2-sqrt((2*a^2+2*c^2)^2-8*(b^2-a^2)^2-8*(b^2-c^2)^2))
(If P is outside the square)
This results in (for Problem2):
x = 0.5*sqrt(260 + 28*sqrt(17)) if P is inside the square and
x = 0.5*sqrt(260 - 28*sqrt(17)) if P is outside the square.
These forms are indeed a lot simpler.
Use P inside the square (both solutions will be found this way.) Divide
the square into four rectangles, with internal corners at P. Let the
side-lengths of the rectangles be w, x, y, z, with w+x = y+z = AB.
Pythagorus shows us:
w^2 + y^2 = AP^2
w^2 + z^2 = BP^2
x^2 + z^2 = CP^2
x^2 + y^2 = DP^2 = AP^2 + CP^2 - BP^2
So DP = sqrt(AP^2 + CP^2 - BP^2)
To solve for AB, let x=AB, let point P be at (Px, Py), A be at (0,0),
B be at (0,x), and let a=AP, b=BP, c=CP, d=DP. Then:
(1) Px^2 + Py^2 = a^2
(2) Px^2 + (Py-x)^2 = b^2
(3) (Px-x)^2 + (Py-x)^2 = c^2
(4:2-1) Py = [x^2 - (b^2 - a^2)]/2x
(5:3-2) Px = [x^2 - (c^2 - b^2)]/2x
(6:4,5->1) 2x^4 - 2x^2(a^2+c^2) + (b^2-a^2)^2+(c^2-b^2)^2 = 0
Quadratic Formula:
x^2 = [ (a^2 + c^2) +/- sqrt( (2bd)^2 - (a^2 - c^2)^2 ) ] / 2
For Problem 1, DP = sqrt(17), AB = 1 or 5
For Problem 2, DP = 11, AB = sqrt(65 +/- 7sqrt(17))
Update 2 Sept. 2008: Bojan Basic writes:
I just want to inform you that this is a very hard problem. In fact, it is well-known and still unsolved. You may check chapter D19 of Guy's book "Unsolved Problems in Number Theory" for much informations about it. If you don't have that book, its status can be seen here: http://mathworld.wolfram.com/RationalDistanceProblem.html.