Ken's POTW
Cards in a Circle
What is the radius of the smallest circle that can enclose all 52
non-overlapping cards of an ordinary deck of playing cards?
And what is the configuration of the cards? Assume the smaller
dimension of the cards is 5 and the larger is 7 (this is the
ratio I found of my Bicycle deck.)
Source: Original.
11/29/06. A puzzle forum stated this same question and found a smaller answer. I copy the result
here exactly as it was found on the website:
wu::forums. The lowest radius found was 25.94, with the following configuration:
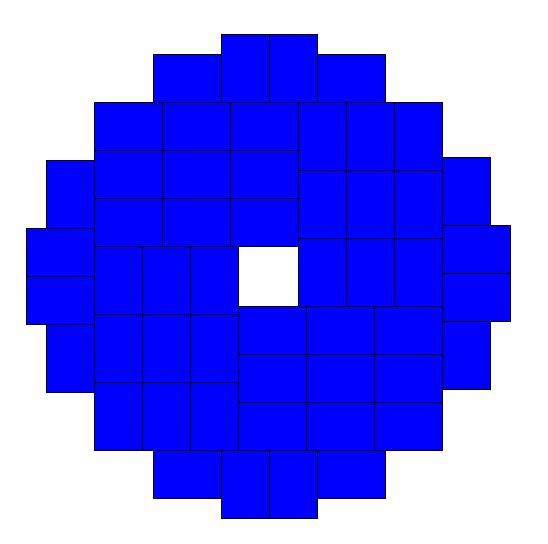
Many solutions were received, and I list them here in order of increasing
radius, because they were all cleverly done.
From
Radu Ionescu:
OK! I try to describe it in words but please scuse me my english.
-
First I construct a retangle with 40 cards (40x35) in a 8x5 arrangement and
I placed four cards length-wise along each two side (of 40) and two cards
length-wise along each two side (of 35). (40+2x4+2x2=52)
-
I calculate R=sq(17.5^2+20^2)=26.57
-
I verified the distance from the of retangle to the two different summits:
-
D1=sq(25^2+7^2)=25.96<26.57 OK!
-
D2=sq(22.5^2+14^2)=26.5<26.57 OK!
From
Leendert Biemans:
[I think there may be a slight mis-count at the beginning - it
seems there's a 6*8=50, but all cards are accounted for in the
end. - KD]
With 52 cards we can conclude that the center of the figure has to
contain a 'solid' figure with all cards in a 'square' as possible
figure.
When we use only 50 cards be can lay a figure that is 42*40 units
(6*7 and 8*5)
This leaves us with two card. But alas the circle now has a
radius of 29=sqrt(20^2+21^2)=sqrt(841) we can easily place the two
cards with their long sides next to the square withing the circle.
Hence we can even use the short sides to attach them to the square.
If we want we can even place four card extra cards due to the fact
that the circle parts are big enough to hold them easily. This
gives us the impression we could use the edge cards to maybe
tighten the circle giving the the following picture:
(the < and ^ direct to the smallest side of a card)
+--+
|< |
+-+-+-+-+-+-+
|^|^|^|^|^|^|
+-+-+-+-+-+-+-+-+
+-|^|^|^|^|^|^|^|^|-+
|^+-+-+-+-+-+-+-+-+^|
++-|^|^|^|^|^|^|^|^|-++
|< +-+-+-+-+-+-+-+-+< |
a++-|^|^|^|^|^|^|^|^|-++
|^+-+-+-+-+-+-+-+-+^|
b+-|^|^|^|^|^|^|^|^|-+
+-+-+-+-+-+-+-+-+
c |^|^|^|^|^|^|
+-+-+-+-+-+-+
d |< |
e+--+
Now searching for the solution we have to find the largest distance
of one edge to the center of the figure.
a = sqrt(2,5^2 + (4*5+7)^2) = sqrt(735,25)
b = sqrt((7+2,5)^2 + (5*5)^2) = sqrt(715,25)
c = sqrt((2*7)^2 + (4*5)^2) = sqrt(596)
d = sqrt((3*7)^2 + (3*5)^2) = sqrt(666)
e = sqrt((5+3*7)^2 + 3,5^2) = sqrt(668,25)
This brings the 'largest/smallest-radius' back to sqrt(735,25).
It is not 'wise' to remove another card from the 'edge' of the
center square. All we could try is to create some extra room for
the outer card with edge a. The only possibility for this is to
move the cards on line directly attached to this card.
The new edge coordinates for a and c are then changed ->
a = sqrt(2,5^2 + (3*5+7)^2) = sqrt(490,25)
c = sqrt((2,5+2*7)^2 + (4*5)^2) = sqrt(672,25)
(a is obsolete because i falls below the edge of b look at the picture
below)
The edges are so close together now that is seems impossible to
improve this anwer thus leaving the answer to a circle with radius
sqrt(715,25) [ = 26.74 ]
the figure will look like this:
+--+
|< |
+-+-+-+-+-+-+
+-+^|^|^|^|^|^+-+
|^+-+-+-+-+-+-+^|
+-+-+^|^|^|^|^|^|-+-+
|^|^+-+-+-+-+-+-+^+^|
+++-+^|^|^|^|^|^+-+++
|< +-+-+-+-+-+-+< |
+++-+^|^|^|^|^|^+-+++
|^|^+-+-+-+-+-+-+^|^|
b+-+-+^|^|^|^|^|^+-+-+
|^+-+-+-+-+-+-+^|
c+-|^|^|^|^|^|^|-+
+-+-+-+-+-+-+
d |< |
e+--+
From
Ken H. Burres III:
- With cards that are 5X7, you can make a square consisting of 35
cards (35 x 35 - cards in landscape format (base of 5 cards, height of 7
cards)), for a square is the shape that consists of the largest amount
of area with the smallest perimeter. Unfortunately the circle
encompassiong these cards would not leave room for the other 17.
- A rectangle that is 42 x 40 (b x h respectively) can be formed
adding 13 more cards for a total of 35 + 13 = 48 cards.
- The above rectangle yeilds a raduis of 29 (the ractangle has a
diagonal of length 58: 42^2 + 40^2 = 58^2; so the radius would be the
intersection of the diagonals which bisect each other).
- Here we have four cards left.
- Since the radius is 58 and the height of the rectangle is 40, there
are 9 units on either side of the rectangle to the tip of the circle. A
card could be layed side-ways (landscape) on either side. This leaves 4
units on either side. The same can be done to the other sides.
- Our problem here is whether or not the four cards fit in the
circle. We know they fit by width, but we don't know if the length (7
units) fit.
- This can be determined by examining two different equations. The
circle with radius 29 can be represented as x^2 + y^2 = 841 or
y = sqrt[841 - x^2]. The distance from the center point to the top of
the card added to the height of the would be 25 (1/2 (40) + 5). The top
of the card (length 7 units) could be represented by y = 25. To see if
the card fits, we simply find where these two equations intersect. We
know y = 25. If |x| > (1/2)(7) then the card will fit. Similarly, the
other equation with the other side can be represented with y = 26. Also
similarly if |x| > (1/2)(7) then those cards will fit.
- Evaluating the equations one will find that in the first situation
the intersections are at (+ - sqrt(216), 25), where sqrt(216) > 3.5. In
the second the intersections would be (+ - sqrt(165), 26), where
sqrt(165) > 3.5.
- Therefore I conclude that the smallest possible raduis would be 29
units.
My (Ken's) solution:
-
51 cards can be arranged symetrically: 35 in a 5x7 square,
35 units on a side, with four cards on each side of the square.
This figure has a radius of 26.5.
-
Add the last card by changing one of the sides of four cards to five.
Then the center of the circle is not so easily placed, but through
the following equation, we can find that the radius is 27.54:
r2 =
142
+ y2
= 17.5 2
+ (45-y)2
When I saw the first solution above, I realized I hadn't investigated
how much free space there was on the side of five cards.
Mail to Ken

