The Path of a Billiard Ball

1. A billiard ball starts from one corner of a equilateral triangular pool table. The ball bounces 5 times and returns to the original corner. Find the original angle of travel of the ball. [Let the initial corner be located at the origin and the other corners be (10,0) and (5,5rt3).]
2. Repeat for 7 bounces.
3. For what initial angles will the ball end at the same corner (and how many bounces)?
4. For what initial angles will the ball end at a different corner (and how many bounces)?

Source: Many sources, submitted by Ravi Subramanian.

1. This is impossible. There is no angle that will allow the ball to return to its original corner after exactly 5 bounces. See the answer to questions 3 & 4 below.
2. The ball should be launched at angle arctan(2*sqrt(3)/3) = 49.1 degrees or at angle arctan(sqrt(3)/9) = 10.9 degrees. These angles can be derived from the answer to questions 3 & 4 below, allowing (x,y) to be either (1,4) or (4,1) respectively.
3. (3&4) Let x and y be relatively prime positive integers. Launch the ball at angle arctan( sqrt(3)*y / (2*x+y) ). The ball will reach a corner after bouncing 2*(x+y)-3 times. Which corner is reached is determined by the value of K=(x+2*y) mod 3: If K=0 then the ball returns to the original corner. If K=1, then the ball ends at (10,0). If K=2, the ball ends at (5,5*sqrt(3)).

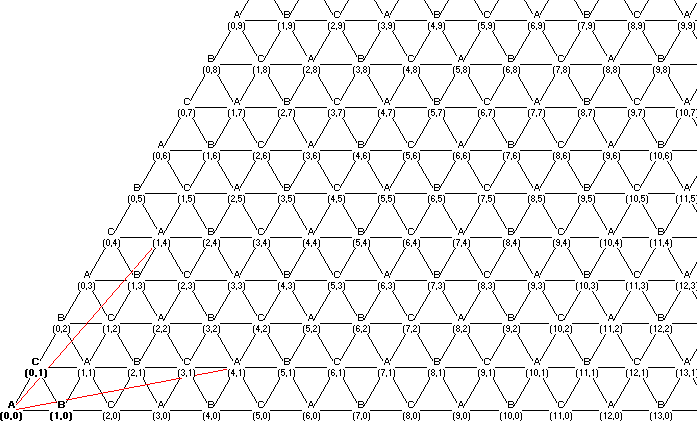
   To see this, tesselate one sixth of the plane with replicas of the billiard table as in the attached diagram. Each vertex of the tesselation is represented by an ordered pair of pseudo-coordinates (x,y). Furthermore, each vertex corresponds to a corner of the original billiard table. A line drawn from the origin to any vertex of the tesselation represents a ball that reaches the corresponding corner. The number of tesselation edges on the diagram which this line crosses is the number of bounces. The red lines on the diagram illustrate the solution to question 2 above.